航空收益管理（七）超售_天富娱乐-天富注册装修站

航空收益管理（七）超售

文章作者：

黄蕾、苏艺、梁哲，同济大学经济与管理学院

上一期的航空收益管理专题介绍了航空公司折扣舱位控制决策，这一期将为大家介绍航空公司另一个增加收益的武器：超售。超售是国际民航界的通行做法，既可满足更多旅客的出行需要，也可避免座位虚耗。

下面就为大家介绍航空公司是如何实施这一有效收益管理举措的。

在航空公司日常运营中，并非所有订座旅客都会在航班起飞时出现，部分订座会在航班起飞前取消，或者未在航班起飞时出现（称为 no-show）。旅客的这些行为会给航空公司带来空置座位损失（称为 Spoilage）。

超售正是为了应对这一问题而诞生的。超售指的是航空公司出售比实际座位数更多的机票。对航空公司而言，超售能够减少空闲座位损失，提高航班客座率，为航空公司带来收益增长。对旅客而言，超售也能满足更多旅客的出行需要，使得更多旅客坐上心仪的航班。

航空公司实施超售的风险显而易见，可能导致到达机场的旅客超过实际座位数。如果经济舱超售，航空公司一般将经济舱的高卡等常旅客（如白金卡、金卡）升舱；如果头等舱/商务舱超售，航空公司只能让部分高舱旅客非自愿降舱；如果整体超售，航空公司只能拒绝部分旅客登机（称为 denied boarding，拒载）。非自愿降舱和拒载可能会导致旅客投诉和超售赔偿，并且会对长期客户关系带来非常恶劣的影响。

航空公司主要从规章制度、经济学效益及服务水平三个方面进行超售决策。

首先，实施超售需要满足规章制度的要求。

民航局于2021年3月出台的《公共航空运输旅客服务管理规定》中新增了“航班超售”一章，该规定对超售的信息告知、征集自愿者（退改签自愿者）程序、优先登机规则、被拒绝登机旅客赔偿等细项进行了明确规定。航空公司需要公布发生超售时的处置方案、旅客拒载细则和补偿措施，并在实际运行中按照方案进行处置。即使如此，航空公司依然面临较大的法律风险。

其次，实施超售需要从经济学角度进行超售数量的决策。

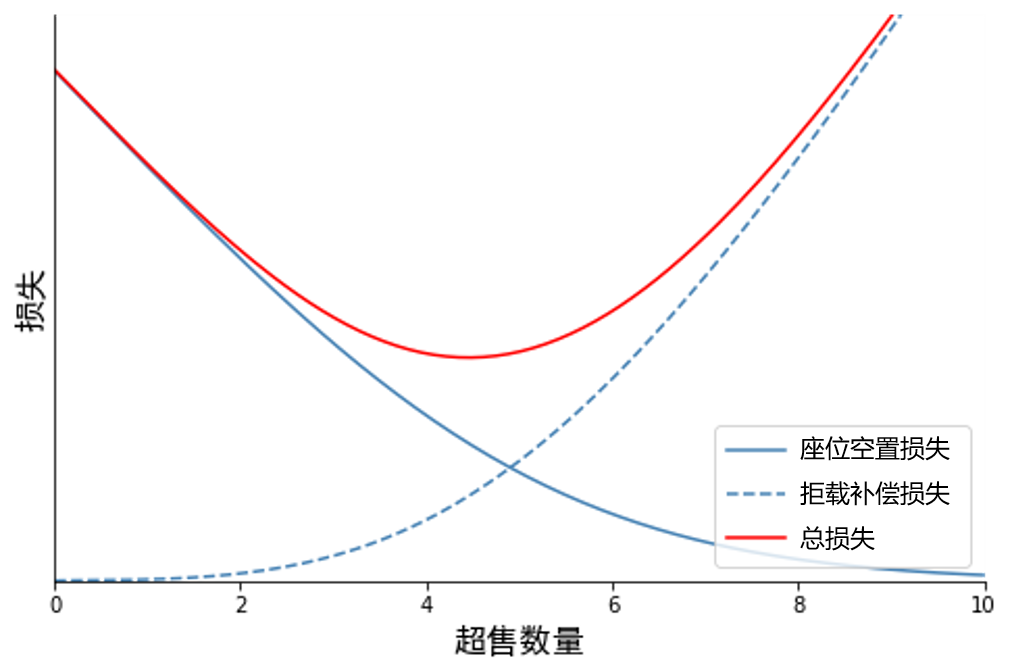
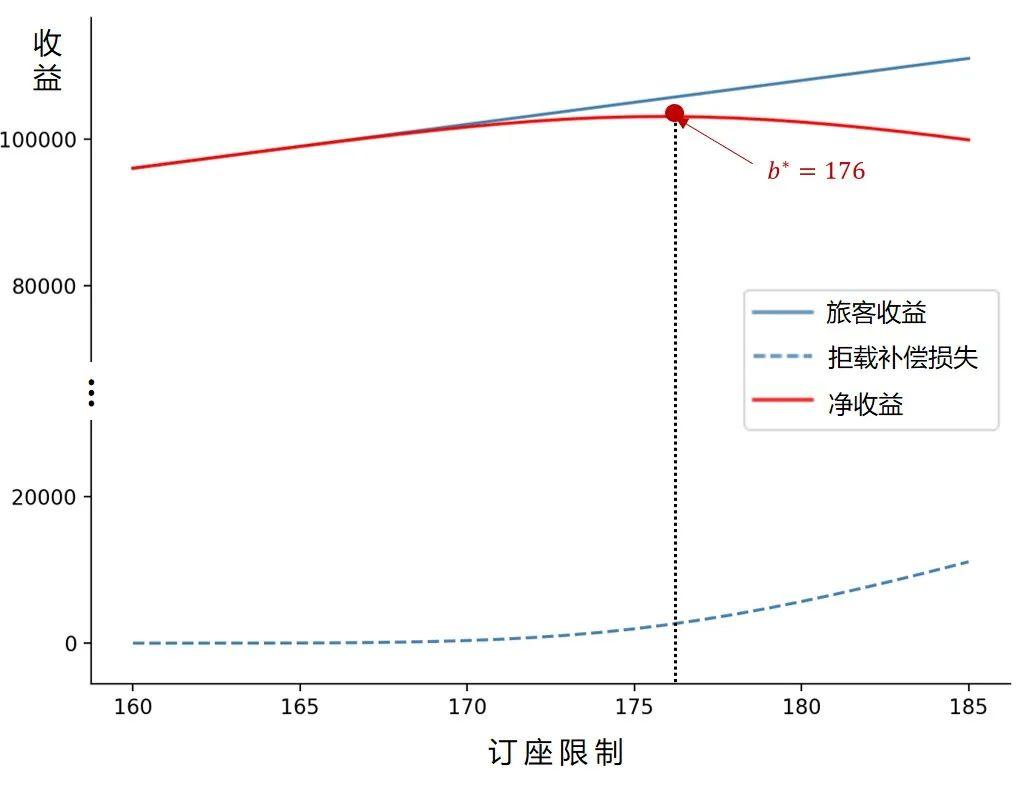
图2展示了超售数量和航空公司损失之间的关系。从图中可以看出，当航空公司增加超售数量时，座位空置损失减少了，但拒绝登机补偿损失增加了。

拒载补偿方式包括票价差额、现金、积分、代金券等等，同时还需要提供后续的航班改签、餐饮以及过夜住宿交通等服务。

因此，航空公司需要平衡空座损失与拒载损失，选择合适的超售数量使得总损失最小。

第三，航空公司需要考虑超售对商誉的影响，设定服务级别约束。

航空公司超售数量越少，则拒载可能性越低，对航空公司商誉与客户关系的影响也越小。因此，航空公司可以设定超售事件发生概率的上限，并根据该阈值来决定超售的数量。这就是航空公司所设定的服务级别约束。

航空公司常常对经济舱综合使用经济学超售模型与服务级别约束，而对头等舱和商务舱设定更加严格的服务级别约束。

下面，我们就为大家介绍航空公司是如何使用模型来支持超售决策的。

超售涉及旅客的取消和no-show行为。我们首先讨论基于旅客no-show行为的超售决策。在进行决策之前，我们需要对旅客no-show的概率进行预测，这一内容在预测下篇中已经介绍过，在此不再赘述。

假定我们需要为一个座位数为 C 的航班进行超售决策，需要决定航班总订座限制（authorization levels，以下记为b）。下面介绍常用的3个模型。

如果假定航班起飞前的所有订座在起飞时出现（show-up）的概率相同，记为 q。（相应的，no-show概率为 1-q。）则很容易想到一种启发式超售决策： $b^*=C/q$ 。

举例：如果 $C=150$ ， $q=0.85$ ，则 $b^*=150/0.85\\approx 176$ 。

最优订座限制为：176

这种模型也称之为确定性模型（Deterministic Model）。确定性模型的优势在于其简单且易于实施，仅需要预测no-show概率，计算方法也非常简单。然而，确定性模型没有考虑拒载成本，并且忽略了旅客no-show行为的随机性，会低估超售风险，产生较为激进的超售决策。

由于该模型易于实施，在航空业有较为广泛的应用，航空公司往往在该模型的基础上调整得到最终的超售决策。

旅客no-show行为往往是随机的而非确定的。考虑这一因素，航空公司可以制定想要的服务级别标准，根据旅客被拒载的概率得到最优的订座限制。

常用的服务级别指标有两种： $s_1$ 与 $s_2$ 。

假定 $Z(b)$ 为旅客订座人数到达订座限制b时show-up的旅客人数。由于航空公司至多接收b个订座请求，则超售风险不会超过 $s_1(b)$ 和 $s_2(b)$ 。

1. $s_1$ :旅客拒载发生的概率：即show-up的旅客人数大于航班实际座位数的概率，记为 $s_1(b)=P(Z(b)>C)$

2. $s_2$ :订座旅客被拒载的比例：即旅客拒载数量与实际show-up旅客人数的比值，记为 $s_2(b)=\\frac{E[(Z(b)-C)^+]}{E[Z(b)]}$ 。

我们可以对旅客no-show行为（或show-up行为）进行一定的统计学假设（如二项式分布），并求得在不同订座水平下的服务水平 $s_1$ 与 $s_2$ 。

接上例，假设旅客出现行为服从二项式分布， $C=150$ ， $q=0.85$ 。

则通过计算可以得到下述的服务水平表（截取了 $x\\in[171,180]$ 的部分数据）：

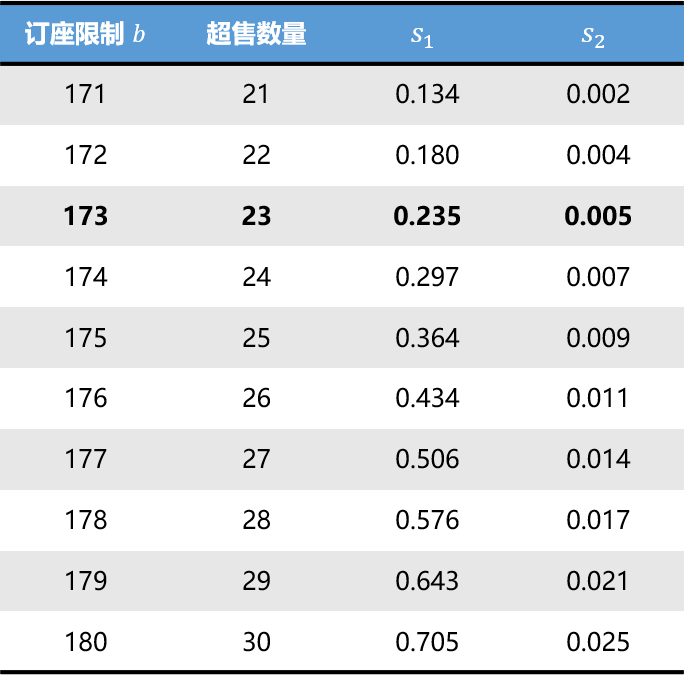
如果我们设定 $s_2=0.005$ 作为服务水平限制，则满足服务水平的最优舱位限制 $b^*=173$ 。同时，我们可以发现确定性模型得到的结果近似位于 $s_1=0.5$ 附近。

经济超售模型通过平衡超售带来的旅客收益增加与拒载成本增加这两个效应，以最大化收益为目标得到最优的超售决策。

在实施经济超售模型前，航空公司需要估计拒载成本（Denied Boarding Cost，下简称DBC），包括赔偿、下一段出行的安排成本，以及等待的食宿成本等。最简单的经济学超售模型假设每个订座的票价相同，忽略票价折扣舱位的影响。下面对该模型进行简单介绍。

简单经济超售模型：

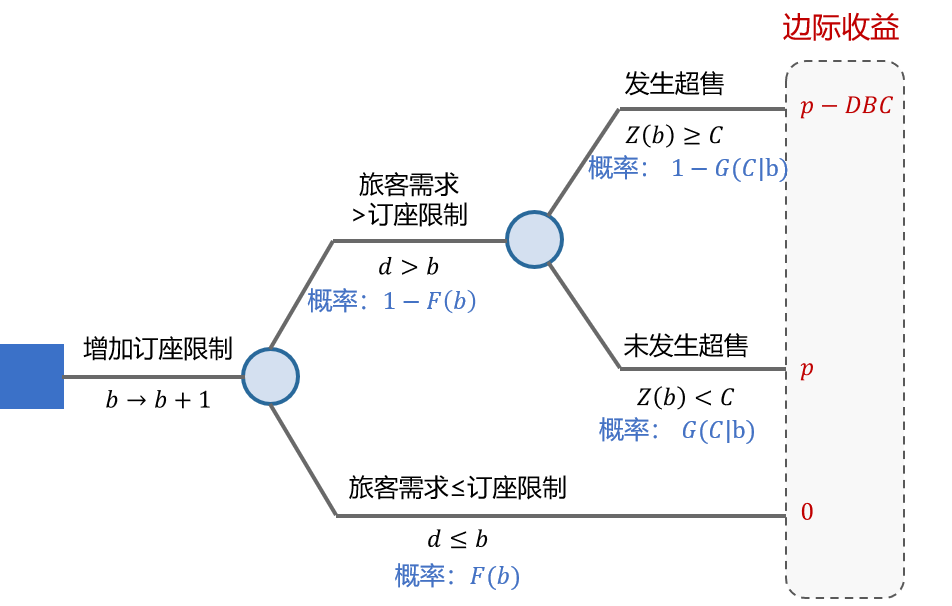
我们通过边际收益来讨论简单经济超售模型的最优解。当航空公司决定最优订座限制 b 时，可以计算增加一个订座限制（b→b+1）的边际收益。当航空公司增加超售数量时，边际收益不断下降。航空公司将不断增加超售数量，直至拒载成本>新增收益。

注：

DBC为拒载成本，Denied Boarding Cost；

p为售出一张票的平均收益；

F(·)为旅客订座需求的累积概率分布函数；

G(·|b) 为订座数为 b 时show-up人数的累积概率分布函数。

从图中可以看到，订座限制的边际收益同时取决于旅客需求与旅客no-show行为。航空公司在设定订座限制之后，旅客的需求被订座限制截断，随后订座旅客在航班起飞之际发生show-up/no-show行为。

1. 如果旅客需求≤订座限制，则增加订座对于收益没有影响

2. 如果旅客需求>订座需求，则接受的订座数量等于订座限制。

a) 如果实际旅客到达数量＞实际座位数，则发生超售，收益变化为 p-DBC

b) 反之，未发生超售，收益变化为 p

通过对图3中的决策树计算可以得到，航空公司将增加订座限制 b 直至 $1-G(C|b)>p/DBC$ ，此时的订座限制为最优超售决策。感兴趣的读者可以参阅参考文献[2]。

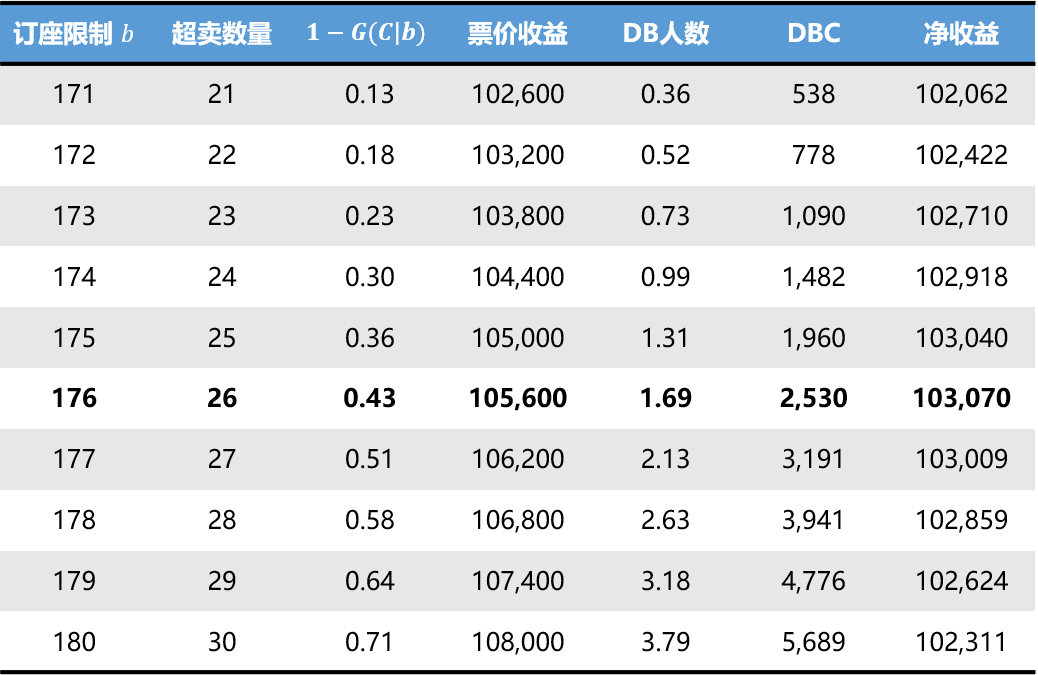
接上例，假设旅客出现行为服从二项式分布， $C=150$ ， $q=0.85$ 。票价 $p=￥600$ ，拒载成本 $DBC=￥1500$ 。可得， $p/DBC=0.4$ 。

假设我们认为旅客需求是无限的，则在不同订座限制下的收益如下表所示，可以看到，当 $1-G(C|b)$ 最接近0.4时，净收益最大，最优订座限制 $b^*=176$ 。

基于上述三种常用的超售模型，航空公司还经常使用混合策略。例如，同时使用经济超售模型与服务级别约束模型，并使用两个限制中较小的作为订座限制。这种混合策略使得航空公司能够在获得经济收益的同时确保服务水平指标在可接受的范围内。

在上述内容中，我们讨论了基于no-show的超售模型。然而，订座取消行为在订座过程中也非常常见，这一行为也会影响收益。例如，在售票过程中，如果旅客订座数量到达订座限制，航空公司可能拒绝部分旅客的需求。然而，当已有订座在后续取消时，也有可能产生座位虚耗。

如果考虑旅客的订座取消行为进行超售，航空公司能够在订座期间动态调整最优的订座限制策略，当然模型也会变的更加复杂。一般而言，旅客订座取消概率是动态变化的，与距离航班起飞日期的时间有关，随着航班起飞日期的临近，订座取消概率断降低。

在这里介绍一种考虑旅客取消的启发式超售模型。

假设航空公司提前购票天数为 $t$ 时的订座取消比例为 $r(t)$ ，接受订座数量为 $b(t)$ ，则大约 $r(t)b(t)$ 的预订会中途取消，而剩余 $(1-r(t))b(t)$ 的预订会保留至航班起飞。

假设航班起飞前旅客show-up概率为q，则基于当前订座，最终的show-up人数为 $q(1-r(t))b(t)$ 。我们可以将 $q(1-r(t))$ 作为动态的show-up概率，并使用上文所述的模型进行求解。

举例，如果航班起飞前20天的取消概率 $r(20)=0.2$ ，前10天的取消概率为 $r(10)=0.1$ ， $C=150$ ， $q=0.85$ 。如果使用确定性模型，则提前20天的最优订座策略为： $b^*(20)=150/[0.85*(1-0.2)]=220$ ，

提前10天的最优订座策略为： $b^*(10)=150/[0.85*(1-0.1)]=196$ 。

超售模型告诉我们，应该如何为航班设定一个最优的总订座限制。然而，航空公司在实施基于折扣票价的舱位控制时会面临困扰，应该如何同时考虑旅客订座与no-show行为，为每个票价子舱位设定购票限制呢？

结合舱位控制的整合模型可以解决这一问题。例如，与上篇推送介绍的EMSR舱位控制算法整合可以得到如下模型：

基于EMSR的整合模型计算步骤如下：

STEP1. 使用超售模型计算总订座限制b，其中 $b\\geq C$

STEP2. 使用EMSR-a或EMSR-b计算各票价子舱位 j 的保护水平 $y_j^*$

STEP3. 根据订座限制 b 计算各票价子舱位 j 的订座限制 $b-y_{j-1}^*$

STEP4. 在订座过程中根据新增订座与取消更新订座限制 b 及各票价子舱位的保护水平

举例，假设 $C=100$ ，使用某一种超售模型计算得到 $b^*=115$ ，销售票价由高至低Y-B-M三个子舱位。计算得Y舱的保护水平为25，B舱的保护水平为55，则可以计算得下表所示的订座限制：

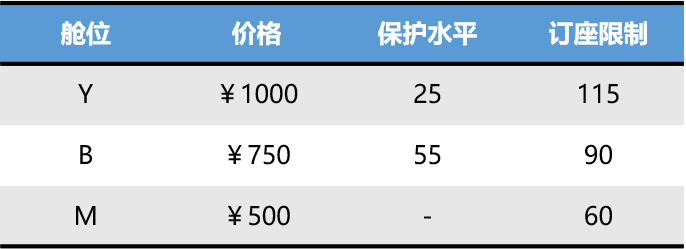
注：以B舱为例，订座限制为115-25=90。

学者也提出了更加复杂的整合模型，例如基于航线网络的整合模型等等，感兴趣的读者可以参阅参考文献[2]。

本期内容首先介绍了航空公司超售的收益和风险，以及航空公司实施超售考虑的因素。之后介绍了几种航空公司进行超售决策的基本模型与拓展模型。

至此，关于收益管理基本内容的介绍也就告一段落了，感谢大家的支持与陪伴。请持续关注我们的后续精彩篇章！

参考：
[1]Phillips, R. L. (2005). Pricing and revenue optimization. Stanford university press.

[2]Talluri, K., & Van Ryzin, G. (2004). Revenue management under a general discrete choice model of consumer behavior. Management Science, 50(1), 15-33.

[3]Vinod, B. (2021). The Evolution of Yield Management in the Airline Industry. Management for Professionals.

[4]Wang, W., & Walczak, D. (2016). Overbooking under dynamic and static policies. Journal of Revenue and Pricing Management, 15(6), 534-553.

[5]交通运输部. (2021). 公共航空运输旅客服务管理规定. http://www.gov.cn/zhengce/zhengceku/2021-03/15/content_5593193.htm

往期回顾：

航空收益管理（一）：概览

（二）：航空市场细分与运价产品设计