大规模神经网络优化：二阶优化器

  • 作者：佚名
  • 来源：网络
  • 时间：2024-06-18 20:55
  • 已有人关注

在本节中，我们将学习一系列二阶优化器。首先我们会比较全面的了解与二阶优化器相关的基础概念。在充分理解这些概念的基础下，我们将很轻松的理解各类二阶优化器。(系列目录）

考虑函数的二阶泰勒展开

f(x+\\Delta x)\\approx f(x)+\ abla f(x)^T\\Delta x+\\frac{1}{2}\\Delta x^T\ abla^2f(x)\\Delta x

当上式取得最小值时，有 \\Delta x=-[\ abla^2f(x)]^{-1}\ abla f(x)。牛顿法即使用更新：\ heta_{n+1}=\ heta_n-\\epsilon H^{-1}\ abla f(\ heta_n)，其中 \ heta 为网络参数，黑塞阵 H=\ abla^2f(\ heta_n)，这里我们简单考虑 H 可逆。在凸函数上对比梯度下降法收敛率 O(1/\\sqrt{\\epsilon})，当初值接近收敛值时，牛顿法有更快的收敛率 O(\\log\\log(1/\\epsilon))。

牛顿法计算黑塞阵（O(n^2)）和矩阵求逆（朴素O(n^3)，当 H 不可逆时需求解 Hs=-\ abla f(x)）的计算复杂度高。

在前面的章节中，我们已经讨论过高斯-牛顿阵是黑塞阵很好的近似。记神经网络为 F=\\sigma\\circ f,f(x,\\cdot):\\mathbb{R}^n\\rightarrow\\mathbb{R}^m,\\sigma:\\mathbb{R}^m\\rightarrow\\mathbb{R}，n 为参数量。则 H\\approx G=J^TH_\\sigma J。其中 H_\\sigma 是函数 \\sigma 对 f(x) 的黑塞阵（形状为 m\ imes m），J 是 f(x) 的雅可比矩阵（形状为 m\ imes n）。通过该方法可以计算雅克比矩阵避免对黑塞阵的计算，同时保证 G 是半正定的。

另一条思路是将 H(\ heta_t) 估计为 B(\ heta_t)，B(\ heta_t) 利用递推的方式从 B(\ heta_{t-1}) 更新。我们可以让 B 为对称正定阵等良好性质便于求得更新值 s，使得 B(\ heta_t)s(\ heta_t)=-\ abla f(\ heta_t)。

联想割线法（secant method）中对梯度的估计，我们有 B(\ heta_k)\\approx\\frac{\ abla f(\ heta_{k}) - \ abla f(\ heta_{k-1})}{\ heta_{k}-\ heta_{k-1}}，注意到 s(\ heta_t)=\ heta_{k}-\ heta_{k-1}，整理可得 B(\ heta_k)s(\ heta_{k-1})=\\Delta \ abla\ heta。在该公式下，根据不同的假设可以得到不同的拟牛顿法。这包括 SR1 方法（symmetric rank-one，假设\\Delta B秩为一），Sherman-Morrison 方法（SR1 基础上直接对逆进行递推），BFGS 方法（假设\\Delta B秩为二），DFP 方法（BFGS 基础上直接对逆进行递推）。其中，BFGS 方法可以保证 B 正定，总时间复杂度为 O(n^2)，记 B(\ heta_{k+1}) 为 B_+，B(\ heta_{k}) 为 B，更新公式为

B_{+}=B-\\frac{Bss^TB}{s^TBs}+\\frac{(\\Delta\ abla \ heta)(\\Delta\ abla \ heta)^T}{(\\Delta \ abla\ heta)^Ts}

然而 O(n^2) 的还是难以接受。L-BFGS 通过储存最近的 k 个 \\{s_i, \\Delta(\ abla\ heta)_i\\}_{i=t-k}^k ，通过每次从初值开始，进行 k 次迭代用 IFQN 算法直接计算 H^{-1}g ，从而降低复杂度到 O(kn) 。但对于神经网络而言还是太大。

黑塞向量积 Hessian-vector-product 是关于 H 的一个基本操作。虽然优化中我们更关注 H^{-1}v，而不是 Hv（v 是[n\ imes 1]的向量）。但该方法在分析神经网络曲面，以及凸函数的共轭梯度法中有应用（虽然在深度学习中梯度存在噪声，共轭梯度法不能保证方向的共轭性，难以应用）。

虽然计算 H 需要 O(n^2) 的复杂度，计算 Hv 只需要 O(n)。在第一次反向传播获得梯度 g 后，将梯度和向量 v 做乘积得到的值 g^Tv 再次进行反向传播，就可以得到 Hv。其原因在于 \\frac{d(g^Tv)}{d\ heta}=\\frac{dg}{d\ heta}^Tv+g^T0=Hv。这里 Hv 的数学含义是方向梯度 \ abla_v f。PyTorch 中的实现为F.hvp。

目前的深度学习框架往往都提供了高效的 vector-Jaccobian-product 和 Jaccobian-vector-product，例如 PyTorch 中的 F.vjp 和 F.jvp。为了计算高斯-牛顿阵与向量的乘积 Gauss-Newton-vector-product（Gv=(J^TBJ)v），第一步可以先计算 g(x)=\\frac{\\partial \\mathcal{L}}{\\partial f(x)}。通过计算 g(x) 雅克比矩阵与向量 v 的乘积（jvp），可得 J_{g(x)}v=\\frac{\\partial L}{(\\partial f(x))^T\\partial f(x)}J_{f(x)}v=BJv。继而计算向量 (BJv)^T 与 f(x) 雅克比矩阵的乘积（vjp），即可得到答案 (BJv)^TJ=(J^TBJv)^T=(Gv)^T。

利用 Hv，我们可以对黑塞阵的对角线元素进行估计。Hutchinson 方法是对实对称矩阵对角线元素的估计方法。令 \\hat h=u\\cdot(Hu)，其中 u 是一个服从于高斯分布 N(0,I_d) 的随机向量，则有 \\mathbb{E}_{u}[u\\cdot(Hu)]=\\mathrm{diag}(H)。

数学推导可参考该中文资料

在第一篇中我们已经定义过费雪信息矩阵（Fisher Information Matrix, FIM）。这里我们从神经网络的视角重新定义一次。一般而言，神经网络旨在建模一个分布p(x|\ heta)（对于判别式神经网络，建模条件分布p(y|x;\ heta)），其中\ heta是神经网络的参数。使用交叉熵损失与最大似然等价，目标为最大化 \\log p(x|\ heta)。定义评分函数 s(\ heta)=\ abla_\ heta\\log p(x|\ heta) 为对数似然函数的梯度（神经网络梯度的负数）。

评分函数有性质 \\mathbb{E}_{p(x|\ heta)}[s(\ heta)]=0。这里要格外注意一点，期望是在分布 p(x|\ heta) 下计算的，而不是在数据集上计算的。记数据分布为 x\\sim \\mathcal{D}，\\mathcal{D}与p(x|\ heta)之间存在差距，随着训练的进行不断减小（训练就是p对\\mathcal{D}的拟合）。故\\mathbb{E}_{x\\sim D}[s(\ heta)] 不一定为零。类似的期望取值之后也要注意。

此时费雪信息阵可以有一个比较直观的定义：FIM 即评分函数（网络导数）的二阶矩。即F=\\mathbb{E}_{p(x|\ heta)}[\ abla_\ heta\\log p(x|\ heta)\ abla_\ heta\\log p(x|\ heta)^T]。由于 \\mathbb{E}_{p(x|\ heta)}[\ abla_\ heta\\log p(x|\ heta)]=0，此时二阶矩就是评分函数的协方差。

在之前我们已经知道 FIM 与 Hessian 的关系，即 F=-\\mathbb{E}_{x\\sim p(x|\ heta)}[H]。但此黑塞阵不是在数据集上计算的。虽然当训练充分，网络拟合的分布接近实际分布时两者应该接近，但一般而言，F 与实际的 \\mathbb{E}_{x\\sim\\mathcal{D}}[H] 的差距有多少呢？

这里我们借助[LLH'23+]中的推导分析判别式网络，证明其 FIM 就是该网络的高斯-牛顿阵，即 F=G。首先，记网络输出为 p(y|x,\ heta)=\\vec p=\ extrm{softmax}(\\vec z),\\vec z=f(\ heta,x)。对 \\vec z 求导可得 \\frac{\\partial L}{\\partial \\vec z}=\\vec p - \\vec y。故在拟牛顿法开头提到的 H_\\sigma=H_{\ extrm{softmax}}=\\frac{\\partial L}{\\partial^2 \\vec z}=\\frac{\\partial \\vec p - \\vec y}{\\partial \\vec z}=\ extrm{diag}(\\vec p)-\\vec p\\vec p^T 与真实类别无关。其中 \ extrm{diag}(\\vec p) 是一个对角阵，对角线上的元素为 \\vec p。

由于 H_\\sigma 与真实类别无关，我们无需按照数据集进行采样，而是可以直接在网络输出的分布 p(y|x,\ heta) 上采样。如此 H_\\sigma=F_\\sigma=\\mathbb{E}_{y\\sim p(\ heta,x)}[\\frac{\\partial L}{\\partial z}\\frac{\\partial L}{\\partial z}^T]。由于 J 是 z 对 \ heta 的雅克比矩阵，与真实标签无关，故 G=J^TH_\\sigma J=\\mathbb{E}_{y\\sim p(\ heta,x)}[J\\frac{\\partial L}{\\partial z}(\\frac{\\partial L}{\\partial z}J)^T]=\\mathbb{E}_{y\\sim p(\ heta,x)}[\ abla L\ abla L^T]=F。

由于在神经网络中，G 是 H 很好的近似，故 F 也是 H 很好的近似。因此，可以用 F 代替 H 进行优化，即 \ heta_{n+1}=\ heta_n-\\epsilon F^{-1}\ abla f(\ heta_n)。但 F 仍然需要 O(n^2) 的储存开销，同时还有按网络分布采样计算梯度，以及计算 F^{-1} 的计算开销。

FIM 阵除了可以看作是对 Hessian 的估计以外，\ heta_{n+1}=\ heta_n-\\epsilon F^{-1}\ abla f(\ heta_n) 本身还具有一个直观的数据解释。单步优化中，我们希望更新方向使损失最小：

d^*=\\arg\\min_{d,D(\ heta,\ heta+d)=\\epsilon}\\mathcal{L}(\ heta+d)

其中 D 是一个空间度量，衡量两个参数的距离。在（最速）梯度下降方法中使用了欧氏距离，可得 d^*=-\\frac{\\epsilon}{{||\ abla_\ heta\\mathcal{L}(\ heta)||}}{\ abla_\ heta\\mathcal{L}(\ heta)}，即负梯度方向。当更新量为 \\epsilon 时，学习率 \\alpha=\\frac{\\epsilon}{{||\ abla_\ heta\\mathcal{L}(\ heta)||}}。

然而我们的目标是最大化似然函数，参数的改变导致似然函数 p 在函数空间的改变。故我们希望使用一个度量 D 衡量函数空间的距离，此时我们可以选择 KL 散度（虽然其不是一个严格的距离），即 D(\ heta,\ heta+d)=\\mathrm{KL}(p(\ heta)||p(\ heta+d))=\\mathbb{E}_{x\\sim p(x|\ heta)}[\\log p(x|\ heta)-\\log p(x|\ heta+d)]。用泰勒展开近似到二阶项可得 \\mathrm{KL}(p(\ heta)||p(\ heta+d))\\approx\\frac{1}{2}d^TFd，进一步可得 d^* 的方向为 \ ilde{\ abla}\\mathcal{L}(\ heta)=-F^{-1}\ abla_\ heta\\mathcal{L}(\ heta)。该项被称作自然梯度，沿该方向的梯度下降被称作自然梯度下降。

我们计算当 KL 散度的更新量为定值 \\epsilon 时，学习率 \\alpha 应该为多少。令 \\Delta \\mathrm{KL}=\\frac{1}{2}(\\alpha\ ilde{\ abla}_\ heta\\mathcal{L})^TF(\\alpha\ ilde{\ abla}_\ heta\\mathcal{L})=\\epsilon，解得 \\alpha=\\sqrt{\\frac{2\\epsilon}{\ ilde{\ abla}_\ heta\\mathcal{L}^TF\ ilde{\ abla}_\ heta\\mathcal{L}}}。我们有：

({\ ilde{\ abla}_\ heta\\mathcal{L}^TF\ ilde{\ abla}_\ heta\\mathcal{L}})^{1/2}=((F^{-1}g)^TF(F^{-1}g))^{1/2}=(g^TF^{-1}g)^{1/2}\\dot=\\lambda(x)

记 v=-F^{-1}g 为自然梯度更新方向，又有：

({\ ilde{\ abla}_\ heta\\mathcal{L}^TF\ ilde{\ abla}_\ heta\\mathcal{L}})^{1/2}=((F^{-1}g)^TF(F^{-1}g))^{1/2}=(v^TFv)^{1/2}=||v||_{F}

其中 \\lambda(x) 被称作牛顿减小项（Newton decrement，F 是 H 的近似），通过计算可以得到牛顿下降法单步更新损失的最大更新值为 \\frac{1}{2}\\lambda(x)^2。而 ||v||_{H} 为牛顿更新步长在黑塞阵下的范数（一些论文中也叫做方向锐度 directional sharpness）。故条件 KL 散度变化为定值，也可以改写为。更新值 -\\alpha\ ilde{\ abla}_\ heta\\mathcal{L}=-\\frac{\\sqrt{2\\epsilon}}{||v||_F}\ ilde{\ abla}_\ heta\\mathcal{L}。

回忆梯度下降的中更新项为 -\\frac{\\epsilon}{{||\ abla_\ heta\\mathcal{L}(\ heta)||}}{\ abla_\ heta\\mathcal{L}(\ heta)}，如果在分母上保留 ||\ abla_\ heta\\mathcal{L}(\ heta)||，那么该梯度下降为归一化梯度下降法（normalized gradient descent）。而带学习率项的自然梯度下降与归一化梯度下降有相同的形式，或许可以称作“归一化自然梯度下降”或“归一化牛顿下降”。

上述各类算法中，我们都再梯度前引入了一个逆矩阵得到形如 P^{-1}\ abla\\mathcal{L} 的更新方向。我们可以称 P 为预条件子（preconditioner）。目前对优化器的设计，主要是对预条件子的设计。当预条件子为对角阵时，P^{-1} 可以很方便的获得。此时也可以看作在每个维度上进行自适应更新（adaptive）\\frac{g_i}{p_i}，比如 Adam 类的优化器以及 Sophia 优化器。预条件子可能能起到一下作用：1.降低方差 2.对高条件数问题鲁棒 3.提供高阶（曲率）信息。

给定列向量 u,v，其外积可以定义为 uv^T=u\\otimes v^T。其中前一项是两个向量的乘积，后一项是两个向量的 Kronecker 积。Kroneckor 积的定义如下：

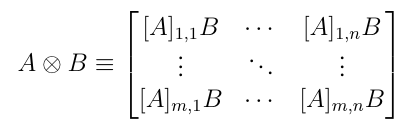
在神经网络中，参数具有结构性质（第i层的参数记为 W_i）。在计算 FIM 阵时，我们把所有的参数平等对待。定义 \ extrm{vec}(\\cdot) 算符将 Tensor W_i 转为为向量（flatten）。Kronecker 积可以方便的表示外积向量化的结果，即 \ extrm{vec}(uv^T)=v \\otimes u。

Kronecker 积有一系列良好的性质：

  1. (A\\otimes B)(C\\otimes D)=(AC)\\otimes(BD)
  2. 对于正定矩阵 A,B，(A\\otimes B)^{-1}=A^{-1}\\otimes B^{-1}
  3. (A\\otimes B)\\otimes \ extrm{vec}(X)=\ extrm{vec}(BXA^T)

K-FAC 算法是自然梯度下降的一种近似实现。定义 MLP 网络中第i层为 a_i=\\phi_i(z_i),z_i=W_ia_{i-1}（为简化不考虑 bias），其中\\phi为激活函数。梯度 \ abla_\ heta\\log p(x|\ heta)=[\ extrm{vec}(\\frac{\\partial\\mathcal{L}}{\\partial W_i})^T]^T。K-FAC 算法使用三个近似以高效的实现自然梯度下降。

近似一：作者利用服从数据集分布的数据来计算二阶矩，进而近似计算 FIM 阵，即 F=\\mathbb{E}_{x\\sim\\mathcal{D}}[\ abla_\ heta\\log p(x|\ heta)\ abla_\ heta\\log p(x|\ heta)^T]\\approx\\frac{1}{N}\\sum_{i=1}^N[\ abla_\ heta\\log p(x_i|\ heta)\ abla_\ heta\\log p(x_i|\ heta)^T]。这里 x_i 是从数据集中采样的数据。但是只有当网络分布接近真实分布时两者才能近似。实际上一个好的估计是经验 FIM 阵：F=\\frac{1}{N}\\sum_{i=1}^N[p(x_i|\ heta)\ abla_\ heta\\log p(x_i|\ heta)\ abla_\ heta\\log p(x_i|\ heta)^T]。然而由于梯度计算是批量进行的，我们只能得到一个批量样本中作为一个整体的 \\frac{1}{B}\\sum_{i=1}^B\ abla_\ heta\\log p(x_i|\ heta)。作者用该近似避免了额外的采样计算开销。

近似二：将每层的参数作为整体，可以把 FIM 阵分块。F_{ij}=\\mathbb{E}[\ extrm{vec}(\\frac{\\partial\\mathcal{L}}{\\partial W_i})\ extrm{vec}(\\frac{\\partial\\mathcal{L}}{\\partial W_i})^T]。又根据链式法则中有 \ extrm{vec}(\\frac{\\partial\\mathcal{L}}{\\partial W_i})=\ extrm{vec}(\\frac{\\partial L}{\\partial a_i}a_{i-1}^T)=a_{i-1}\\otimes \\frac{\\partial L}{\\partial a_i}。结合 Kronecker 积的性质 1 我们有 F_{ij}=\\mathbb{E}[(a_{i-1}\\otimes \\frac{\\partial L}{\\partial \\vec a_i})(a_{i-1}\\otimes \\frac{\\partial L}{\\partial \\vec a_i})^T]=\\mathbb{E}[a_{i-1}a_{j-1}^T\\otimes \\frac{\\partial L}{\\partial a_i}\\frac{\\partial L}{\\partial a_i}^T]。

如果我们维护 F_{ij} 的移动平均作为估计，则需要 O(n^2) 的储存空间。K-FAC 利用近似 \\mathbb{E}[a_{i-1}a_{j-1}^T\\otimes \\frac{\\partial L}{\\partial a_i}\\frac{\\partial L}{\\partial a_i}^T]=\\mathbb{E}[a_{i-1}a_{j-1}^T]\\otimes \\mathbb{E}[\\frac{\\partial L}{\\partial a_i}\\frac{\\partial L}{\\partial a_i}^T] 从而只需维护两个向量的移动平均，即 O(n) 的储存空间。[MG20]主要根据实验说明其效果不错。下图中左图是 F，中间是 F 的近似，右图是两者的差。

近似三：在前向和反向传播中，a_i和\\frac{\\partial L}{\\partial a_i}都是已有的值，故 F 阵已经可以计算了。为了方便计算 F 的逆，作者进一步对 F 阵的结构做了两种假设，分别是块对角（block-diagnoal）矩阵和块三对角矩阵（block-tridiagonal）。这里我们只讨论前者。在该假设下，我们只关心 F_{i,i}，即层内的相关性（假设不同层间弱相关）。根据 Kronecker 积的性质二，我们有 F_{i,i}^{-1}=(a_{i-1}a_{i-1}^T)^{-1}\\otimes (\\frac{\\partial L}{\\partial a_i}\\frac{\\partial L}{\\partial a_i}^T)^{-1}\\dot=A_{i-1,i-1}^{-1}\\otimes G_{i,i}^{-1}。根据性质三，可得自然梯度 F_{i,j}^{-1}\ extrm{vec}(\\frac{\\partial\\mathcal{L}}{\\partial W_i})=\ extrm{vec}(G_{i,i}^{-1}\\frac{\\partial\\mathcal{L}}{\\partial W_i}A_{i-1,i-1}^{-1})。

学习率调整：通过上式计算出自然梯度后，我们还要对自然梯度的学习率进行修正。与之前推导自然梯度下降学习率类似，当 KL 散度的近似值 \ u=\\frac{1}{2}(\\alpha\ ilde{\ abla}_\ heta\\mathcal{L})^TF(\\alpha\ ilde{\ abla}_\ heta\\mathcal{L}) 大于阈值 C 时（[GM16]中选择 0.3）将其裁剪。即学习率\\alpha\\leftarrow\\alpha\\min(1, \\sqrt{\\frac{C}{\ u}})。如此可以限制每次更新时 KL 变化的幅度。其中，\ u 的计算可以通过”黑塞向量积“一节的技术快速计算。作者实际每个几个批量计算一次，进一步降低均摊开销。

其它实现细节：在该方法的一个实现中，作者基于 K-FAC 添加动量时，动量应用在自然梯度上。权重衰减也应该发生在函数空间，故应使用 (F+\\lambda I)^{-1} 作为预条件子，实际中仍然使用参数空间的衰减 \\frac{1}{2}\\lambda\ heta^T\ heta。计算正定矩阵 A 的逆时，可以通过特征值分解 A=Q\\Lambda Q^T，其中 Q 是正交矩阵，\\Lambda 是对角阵，其对角线上的元素为特征值。故 A^{-1}=Q\\Lambda^{-1}Q^T。为了获取前向传播中的 a 和反向传播中的 \\frac{\\partial L}{\\partial a}，可以通过 pytorch 的 hook 功能快捷实现。

缺点：虽然通过三个近似，可以一定程度高效的实现自然梯度下降，然而 K-FAC 算法具有不少缺点。

  1. 通过带噪声的梯度信息近似曲率信息会使高阶信息估计不准确。即使是在大批量（低噪声）的情况下，[MMY+19]通过实验表面 K-FAC 效果不如 SGD。
  2. 三个近似一定程度也损失了精度。
  3. 对于不同的网络结构（如卷积等）需要重新推导，实现较为复杂。

受到 K-FAC 的启发，[GRB21]将拟牛顿法 (L-)BFGS 推广到神经网络上。与 K-FAC 类似，作者在 Kronecker 积以及块对角阵假设的基础下设计了 K-BFGS 算法。由于使用不广，这里不再赘述。

Adaptive 类算法（Adagrad[DHS11], Adam[KB14]等）中的自适应学习率，可以看作是使用了对角阵的预条件子。在该篇内容中，我们还会从别的视角探究这类算法。本篇则从曲率信息的角度进行探究，为了方便这里不讨论权重衰减、动量修正等技术。记梯度为 g_t，预条件子为 P，更新量为 U（梯度下降即 U_t=-\\alpha g_t），A^{1/2}=X,XX=A。

Adagrad 算法在一位参数上的自适应学习率为 -\\frac{1}{\\sqrt{\\sum_{i=1}^tg_i^2}}。而在原始论文中，实际上 Adagrad 的原始形式是 U=-\\alpha({\\sum_{i=1}^tg_tg_t^T})^{-1/2}g_t=-\\frac{\\alpha}{\\sqrt{t}}(\\frac{1}{t}\\sum_{i=1}^tg_tg_t^T)^{-1/2}g_t。这里我们采取与原论文不同的分析方法。注意到 K-FAC 中的近似一，即用数据分布近似计算 FIM 阵。我们同样可以将 Adagrad 看作是近似 FIM 阵的预条件子加上随时间的梯度衰减，即 P^{-1}=-\\frac{1}{\\sqrt{t}}(\\frac{1}{t}\\sum_{i=1}^tg_tg_t^T)^{-1/2}=-\\frac{1}{\\sqrt{t}}F^{-1/2}。这里预条件子使用了 F^{-1/2} 而非 F^{-1}，这与曲率之间能否建立联系呢？

在归一化自然梯度下降中，我们通过设定学习率 \\alpha=\\sqrt{\\frac{2\\epsilon}{g^TF^{-1}g}} 让每步的更新幅度相等。在学习率与动量一章中，我们讨论过高条件数对优化的不利影响。考虑 F\\approx H 的特征值 \\lambda_i 对应的特征向量 e_i，如果我们希望对每个特征向量进行伸缩变换，使 ||s_ie_i||_H 相等，从而让不同特征值对应的更新幅度相等。令 ||s_ie_i||_H=\\frac{1}{2}(s_ie_i)^TF(s_ie_i)=\\epsilon，解得 s_i=\\sqrt{2\\epsilon\\lambda_i}。记梯度 g 在 e_i 上的分量为 d_i，此时 -U=F^{-1}\\sum_i s_i\\cdot d_ie_i=\\sum_i \\sqrt{2\\epsilon\\lambda_i}\\cdot \\frac{d_i}{\\lambda_i}e_i=\\sqrt{2\\epsilon}\\sum_{i}\\frac{1}{\\sqrt{\\lambda_i}}d_ie_i。对比 F^{-1}g=\\sum_i\\frac{1}{{\\lambda_i}}d_ie_i，我们发现特征值进行了开根，故我们可以选择 F^{-1/2} 作为预条件子以满足 s_i 的选择。由此可见，Adagrad 算法（以及不包括 \\frac{1}{\\sqrt{t}} 学习率衰减的 Adam 算法）可以看作是”特征值归一化的自然梯度下降“。

Adagrad 中继续将 P 限制为对角阵，这样可以减小 P 的储存空间、求逆以及开方的复杂度。由于 g_tg_t^T 的对角线构成的矩阵为 \\mathrm{diag}(\\sum_{i=1}^tg_{i,j}^2)_{j=1}^n，其中 g_{t,i} 是第 i 个参数的导数。故 P^{-1}=-\\frac{1}{\\sqrt{t}}F^{-1/2}=-\\frac{1}{\\sqrt{t}}\\mathrm{diag}(\\frac{1}{\\sqrt{g_{t,i}^2}})。

从曲率的角度看，Adaptive 类算法实际上是利用数据分布近似的对角 FIM 阵（牛顿阵）下的特征值归一化的自然梯度下降（或牛顿梯度下降）。

Shampoo 算法[GKS18]是对 Adagrad 更新量的近似计算。记 Adagrad 的更新量为 V^{-1/2}g,V=\\sum_{t=1}^Tg_tg_t^T 是对 \\sqrt{t}F 的近似计算。V 矩阵是一个[nxn]的矩阵，储存、求逆、求方根开销都很大。如果使用对角近似，我们可以看成在每个位子上使用了[1x1]的矩阵，大量减小了开销，然而丢失了大量信息。那能否在这两者之间取得一个平衡呢？

一个简单的思路是类似 K-FAC 一样使用块对角矩阵，即只考虑每层参数内的相关性。对于第 l 层参数 W_l，g_l 为该层导数，G_l 是 g_l 重整（reshape）成与 W_l 形状相同的矩阵。则更新公式为 W_{t+1}=W_t-\\alpha (\\sum_{t=1}^Tg_lg_l^T)^{-1/2}g_l\\dot=W_t-\\alpha V_l^{-1/2}g_l。但这样做需要维护一个 O(m^2n^2) 矩阵以及对其求逆和求方根，仍然是不小的开销。

Shampoo 算法将 V_l^{-1/2}g_l 进行近似，这里我们只做直观理解，理论证明可以参考原论文。对于形如[m\ imes n]的二维矩阵 W_l，令 L_t=\\sum_{t=1}^TG_lG_l^T ([m\ imes m])，R_t=\\sum_{t=1}^TG_l^TG_l[n\ imes n]，更新为 W_{t+1}=W_t-\\alpha L_t^{-1/4}G_tR_t^{-1/4}。其中 -\\frac{1}{4}+-\\frac{1}{4}=-\\frac{1}{2}，与 Adagrad 中的次数相同。如此一来，我们只需要维护 O(m^2) 和 O(n^2) 的矩阵，以及对其求逆和求方根。这样大大减小了计算开销。

对于一般的张量 W_t 有形状[n_1\ imes n_2\ imes\\cdots\ imes n_k]，总大小为 n。维护 k 个矩阵，每个矩阵是 H_l^{(i)}=\\sum_{t=1}^TG_l^{(i)}G_l^{(i)T}。这里 G_l^{(i)} 是 g_l 重整成[n_i\ imes \\frac{n}{n_i}]形状的矩阵。如此一来，H_l^{(i)} 有形状[n_i\ imes n_i]。为了计算最后的更新量，将 G_t 轮流 重整成[\\frac{n}{n_i}\ imes n_i]形状的矩阵，计算 G_t\\leftarrow H_l^{(i)-1/2k}G_t，再将其 reshape 成原状。此时总次数为 k\ imes-\\frac{1}{2k}=-\\frac{1}{2}，与 Adagrad 中的次数相同。维护的矩阵大小为 O(n_i^2)，与直积计算整层的 A_t 相比减小了计算开销。

[YGS+21]放弃了 K-FAC 和 Adagrad 中的近似一，并估计为对角矩阵。其通过上文提到的 Hutchinson 方法估计 H 的对角阵 D，维护梯度动量 m_t 和对角阵动量 D。使用与 Adam 一致的更新方式，即 D^{-1/2}m_t，在每个维度上更新方向为 \\frac{m_t^i}{\\sqrt{d^i_t}}。

在此基础上，AdaHessian 还用平均池化将 H 的值进行平滑，从而使训练更稳定。

Sophia 算法[LLH'23]在 AdaHessian 算法的基础上进行了改进。首先，其通过真实的 F 函数对 H 进行了估计。根据“费雪信息阵与牛顿法”一节的内容，计算 F 时损失函数应使用按照网络输出概率采样的真实标签，即

F=\\mathrm{diag}(\\mathbb{E}_{y\\sim p(y|x;\ heta)}[\ abla_\ heta\\mathcal{L}_\ heta(x,y)\ abla_\ heta\\mathcal{L}_\ heta(x,y)^T])=\\mathbb{E}_{y\\sim p(y|x;\ heta)}[{\ abla_\ heta\\mathcal{L}_\ heta(x,y)\\cdot\ abla_\ heta\\mathcal{L}_\ heta(x,y)}]

注意到实际训练中我们无法得到单个样本的 \\mathbb{E}_y[\ abla_\ heta\\mathcal{L}_\ heta(x,y)]，只能得到一个批量的 \\hat G_B=\\frac{1}{B}\\sum_{b=1}^B\\mathbb{E}_y[\ abla_\ heta\\mathcal{L}_\ heta(x_b,y)]。不过幸好由于 \\mathbb{E}_y[\ abla_\ heta\\mathcal{L}_\ heta(x_b,y)]=0，我们有

F=\\mathbb{E}_y[\\frac{1}{B}\\sum_{b=1}^B\ abla_\ heta\\mathcal{L}_\ heta(x_b,y)\\odot\ abla_\ heta\\mathcal{L}_\ heta(x_b,y)]=\\mathbb{E}_y[\\frac{1}{B}\\sum_{b=1}^B (B\\cdot \\hat G_B)\\odot(B\\cdot\\hat G_B)]=B\\cdot\\mathbb{E}_y[\\hat G_B\\odot \\hat G_B]

由于该操作需要额外的一次反向传播，作者通过每隔 k 步采样一次的方式进行近似，并做动量更新，从而降低了计算开销。

此外，Sophia 没有使用 Adam 中 -1/2 次的“特征值归一化”，而是直接使用自然梯度下降，即 F^{-1}g。为了应对自然梯度下降训练的不稳定性，作者对更新值进行裁剪，使其不超过给定的阈值。

[DHS11]Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
[KB14]Adam: A Method for Stochastic Optimization
[MG15]Optimizing Neural Networks with Kronecker-factored Approximate Curvature
[GM16]A Kronecker-factored approximate Fisher matrix
for convolution layers
[GKS18]Shampoo: Preconditioned Stochastic Tensor Optimization
[MMY+19]Inefficiency of K-FAC for Large Batch Size Training
[GRB21]Practical Quasi-Newton Methods for Training Deep Neural Networks
[YGS+21]AdaHessian: An Adaptive Second Order Optimizer for Machine Learning
[LLH'23+]Sophia: A Scalable Stochastic Second-order Optimizer for Language Model Pre-training

上一篇：android底层优化什么意思,华为所谓的“优化”到底是什么意思 看完这段你就明白...

平台注册入口